Study of tissue inhomogeneity effects on central axis radiation beam parameters using monte Carlo methods
Santhosh VS.1*, Anand RK.2
DOI: https://doi.org/10.17511/ijmrr.2020.i05.03
1* Santhosh VS, Assistant Professor, Department of Radiation Physics, Government Medical College, Thiruvananthapuram, Kerala, India.
2 Anand RK, Assistant Professor, Department of Radiation Physics, Government Medical College, Thiruvananthapuram, Kerala, India.
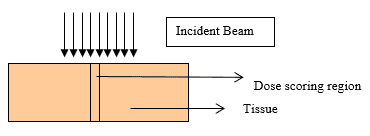
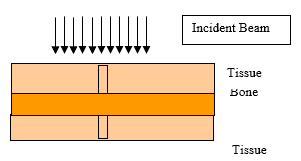
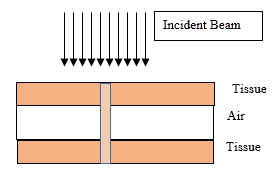
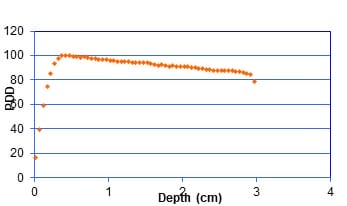
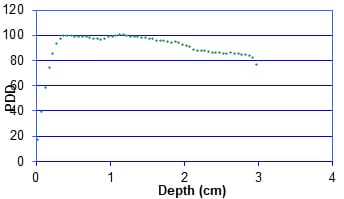
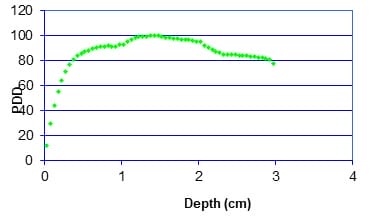
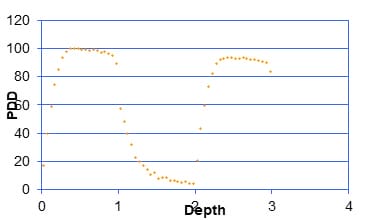
Introduction: The central axis radiation beam parameters are used for the dose calculations in radiotherapy and usually measured in a homogeneous medium. Human body is not homogeneous in nature and the incident beam has to travel through different medium such as bone tissue air etc to reach the tumor. Objective: The objective of the present work is to study the effects of tissue Inhomogeneity on central axis beam parameter such as percentage Depth Dose using Monte Carlo Methods Materials and Methods: The Monte Carlo simulation is a virtual experiment and can be conducted with the Monte Carlo software tool installed in a PC. Input files are written as per the specification of the Monte Carlo code. Two radiation beams beans commonly used for radiation treatment such as Cobalt 60 and 6MV X ray were used for the simulation. Results: Depth Dose characteristics in homogeneous tissue medium for Cobalt60 and 6MV X rays beams were studied and is consistent with the published experimental values.In the second case, at the interface between tissue and bone the PDD pattern changed as reported by the previous works. And the absorbed dose at bone layer is higher than the dose value predicated in a homogeneous condition. In the next simulation we conducted the simulation for a tissue air tissue medium. Conclusion: The present study clearly demonstrate that Monte Carlo methods simulation can be used as a tool for estimation of dose in tissue Inhomogeneity where measurements are seldom possible.
Keywords: Tissue inhomogeneity, Monte Carlo methods, Percentage Depth Dose, Radiotherapy
| Corresponding Author | How to Cite this Article | To Browse |
|---|---|---|
| , Assistant Professor, Department of Radiation Physics, Government Medical College, Thiruvananthapuram, Kerala, India. Email: |
Santhosh VS, Anand RK. Study of tissue inhomogeneity effects on central axis radiation beam parameters using monte Carlo methods. Int J Med Res Rev. 2020;8(5):352-362. Available From https://ijmrr.medresearch.in/index.php/ijmrr/article/view/1212 |


 ©
©